How to transform vibration data accelerometer in power spectrum usign fft?

#1

Hi everybody

I’m developing a project that involves using an accelerometer to collect vibrations from a component, in order to use it as a feature for my predictive calculations.
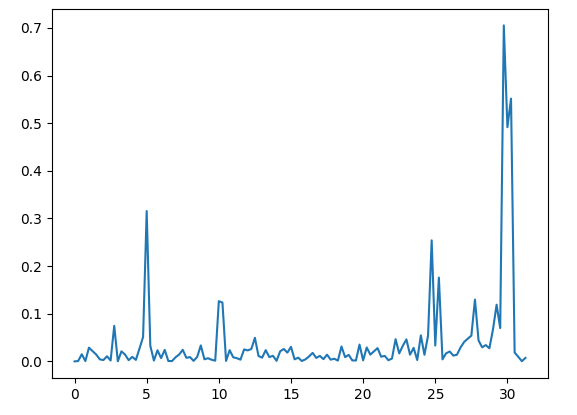
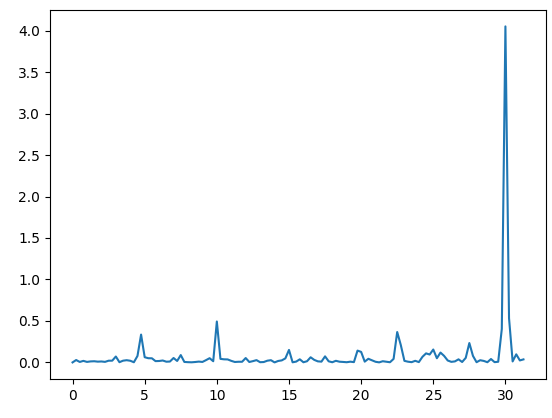
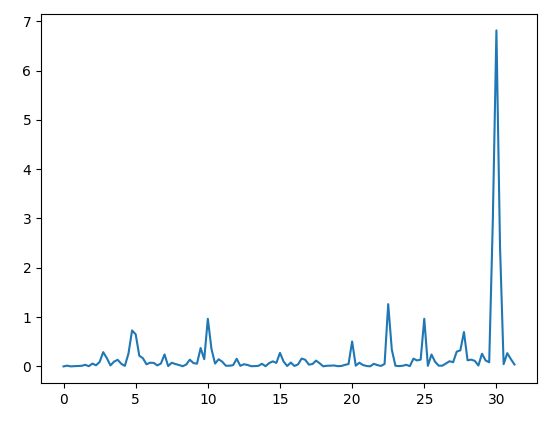
However, I wanted to understand how Edge Impulse transforms the raw accX, accY and accZ data into various features such as accX power spectrum, accY power spectrum and accZ power spectrum. Here is the attachment I want to get:

accX Spectral Power 21.36 - 21.61 Hz
accY Spectral Power 11.11 - 11.35 Hz
accZ Spectral Power 17.94 - 18.19 Hz
.........................................................
accZ Spectral Power 30.15 - 30.4 Hz
accX Spectral Power 19.17 - 19.41 Hz
accX Spectral Power 10.62 - 10.86 Hz

I’ve been reading the documentation GitHub - edgeimpulse/processing-blocks: Signal processing blocks but I haven’t been able to select the key part of what I want. So I looked for other sources like stackoverflow and scipy signal.

The results I got were these:
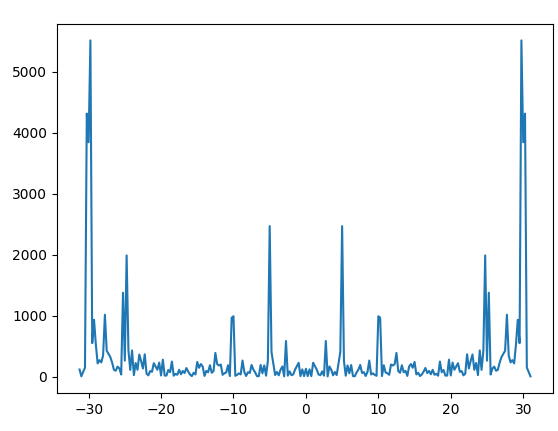
image

I don’t know if this graph makes sense for what I want to get, which would be the power spectrum

data = dado['accX'].values
ps = np.abs(np.fft.fft(data))**2

time_step = 1 / 62.5 # sampling frequency
freqs = np.fft.fftfreq(data.size, time_step)
idx = np.argsort(freqs)

plt.plot(freqs[idx], ps[idx])
plt.show()

Imagine that, given inputs with the following table:
accX accY accZ
0 … … …
1 … … …
2… … …
how do I calculate the power spectrum in order to add to this table so that it can be used in a support vector machine model

accX accY accZ accxPowerSpectrum accyPowerSpectrum ...

0 … … …
1 … … …
2 … … …

#2

Hi @renansaraiva.sdao , thanks for submitting the question

Perhaps @AlexE could chime in?

#3

Hi @renansaraiva.sdao , we just directly feed the output of the fft (the power, or abs, of each bin, not the complex format) into the learn block. If you have filtering on, we will remove bins in the stop band. If you have more samples in the window than your FFT size, then we work similar to a periodogram or Welch’s method…except instead of averaging each FFT bin, we take the max

We also encode some statistics as features…see the source code for their exact position in the feature array

#4

Eu estive a usar:

# f contém os componentes de frequência
# S é o PSD
(f, S) = periodogram(janela, freq_sample, scaling='densidade')
# plotagem:

accX
image
accY
image
accZ
image

Então aplicando:

spectral = []
    for i in range(0, len(S)-4, 4):
        print(i+4)
        spectral.append(scipy.integrate.simps(S[i:i+4]))
    print(f"Spectral (len={len(spectral)}) = {str(spectral)}")

priting:

image
image961×87 4.89 KB

when adding the integration of the PSD areas in the interval 1 in 1, it is noticed that the spectrum of the accZ axis is larger than the accX and accY axes, which should be smaller.

image
image881×53 2.28 KB

#5

We don’t use Welch’s method, and we don’t use a method that exists inside scipy.signal.periodogram, thus results won’t match. Please refer to the source code in the first post and you can see exactly how we reduce the FFTs from the frames into a single periodogram-like output